kNN and Curse of Dimensionality
October 12, 2024
K-Nearest Neighbors is one of the simplest non-parametric classifiers. A non-parametric classifier does not have a fixed number of parameters. Parametric classifiers, like linear regression, have a fixed number of parameters. A KNN model simply looks at its K nearest neighbors and assigns the most common label among them. It is a memory-based or instance-based learning algorithm.
The probability of a class \( y = c \) given a data point \( x \), dataset \( D \), and K neighbors is defined as:
\[ p(y=c|x,D,K)=\frac{1}{K} \sum_{i \in N_k{x,D}} I(y_i=c) \]Here, \( N_k \) represents the indices of the K-nearest points to \( x \) in dataset \( D \), and \( I(.) \) is an indicator function. To find the nearest neighbor, KNN uses a distance metric, with Euclidean distance being the most commonly used.
Curse of Dimensionality
KNN does not perform well with high-dimensional data due to the curse of dimensionality. As the number of dimensions increases, the notion of distance loses its effectiveness.
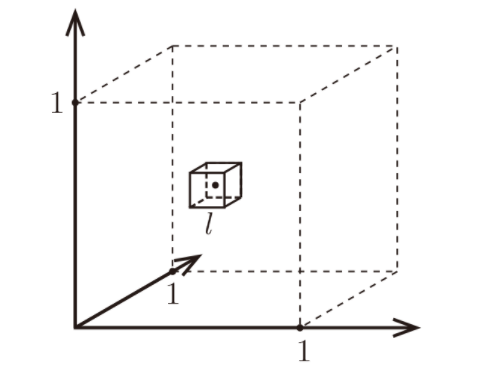
Consider \( N \) data points, each with \( d \) dimensions, uniformly distributed in a unit cube space with features normalized between 0 and 1. To classify a test point \( x \), KNN grows a hypercube inside the space such that it contains the desired number of K neighbors.
Let's assume we are looking at 10 nearest neighbors:
\[ x \in [0,1]^d, K=10 \]Let \( l \) be the length of the hypercube required to contain K nearest points, then:
\[ l^d = \frac{K}{N} = \left(\frac{K}{N}\right)^{\frac{1}{d}} \]For example, if we have \( N=1000 \) samples, the following table illustrates how \( l \) changes with dimension \( d \):
| Dimension (d) | l (Hypercube length) |
|---|---|
| 2 | 0.1 |
| 10 | 0.63 |
| 100 | 0.955 |
| 1000 | 0.9954 |
For 1000-dimensional data points, we need to cover 99.54% of the space to include only 10 nearest neighbors. Not so near, ehh? This means that in high-dimensional spaces, the concept of 'nearest neighbors' loses meaning.